Untuk menghitung jarak antara sebuah titik dan sebuah lingkaran, kita perlu terlebih dahulu menentukan pusat dan jari-jari lingkaran tersebut.
Diberikan persamaan lingkaran: \[ x^2 + y^2 – 4x – 2y – 31 = 0 \] Untuk memudahkan, kita akan lengkapi kuadrat untuk menemukan pusat dan radius lingkaran. Mulai dengan memisahkan variabel: \[ x^2 – 4x + y^2 – 2y = 31 \] Lengkapi kuadrat untuk masing-masing variabel: \[ (x^2 – 4x + 4) + (y^2 – 2y + 1) = 31 + 4 + 1 \] \[ (x – 2)^2 + (y – 1)^2 = 36 \] Dari ini, kita lihat bahwa pusat lingkaran adalah \( (2, 1) \) dan radiusnya adalah \( 6 \). Jarak dari titik \( (8, -7) \) ke pusat lingkaran \( (2, 1) \) dihitung dengan: \[ \sqrt{(8 – 2)^2 + (-7 – 1)^2} = \sqrt{6^2 + (-8)^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \] Jarak dari titik ke lingkaran adalah jarak titik ke pusat dikurangi radius: \[ 10 – 6 = 4 \] Jadi, jarak antara titik \( (8, -7) \) dan lingkaran adalah 4 satuan.
Jarak dari titik (8, -7) ke lingkaran yang diberikan oleh persamaan x² + y² – 4x – 2y – 31 = 0 adalah 4 satuan. Ini merupakan jarak terpendek dari titik tersebut ke permukaan lingkaran.
Sulit juga yang mengerjakan soal matematikan melalui artikel, jadi hasilnya 4. Sekian dari analiswinter.com, terimkasih.

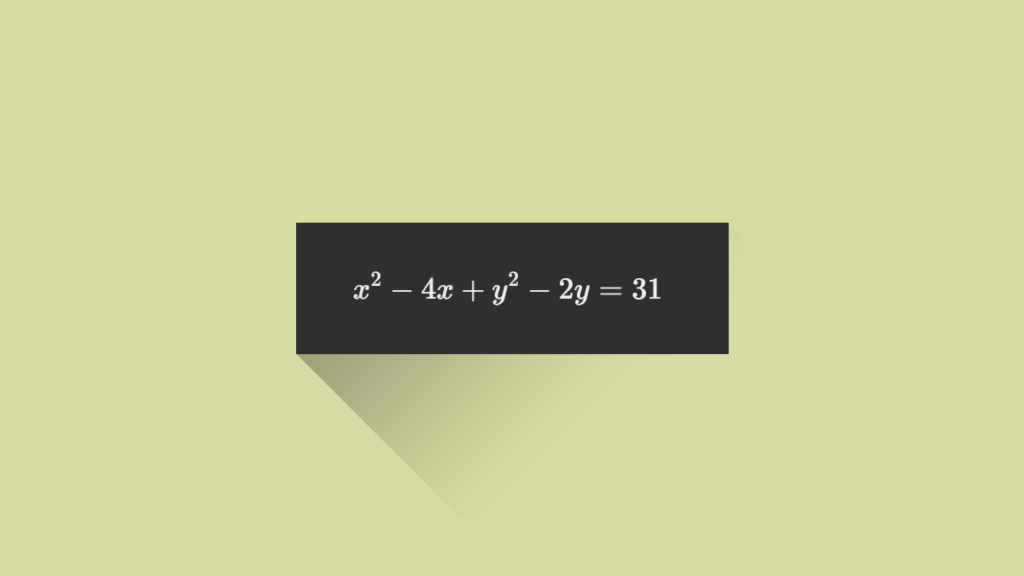





Komentar